AMICS DE LA CIÈNCIA

En esta página esta dedicada para aquellos que quieran dar una idea empresarial, tratar un tema filosófico, psicológico o literario, o bien redactar una parte de alguna obra literaria interesante o bonita, sea extraida de alguna obra literaria o sea de cosecha própia.

Por ejemplo el siguiente trabajo elaborado por dos estudiantes de económicas:

J. P. Muñoz Fernández y J. L. López Espinosa han presentado el siguiente trabajo oteniendo una buena cualificación en la facultat de Económicas de la Universidad de Barcelona :

El Modelo de Equilibrio General Competitivo describe una economía compuesta de agentes maximizadores de funciones objetivo: cada consumidor tiene su propia función de demanda así como cada productor presenta su propia función de oferta. En presencia de precios exógenos, la existencia de un Equilibrio General Competitivo tiene la propiedad de que las utilidades marginales ponderadas de todos los bienes son iguales, y además, iguales que los costes marginales de producción de cada uno de estos bienes. Es decir, se fundamenta en el hecho de que los consumidores y las empresas alcanzan conjuntamente el nivel de satisfacción que deriva, respectivamente, de la máxima utilidad y el máximo beneficio, y por tanto no hay deseo que tiendan a hacer cambiar esta situación.

El denominado análisis de equilibrio general, tiene por objeto indicar explícitamente los nexos que existen entre los distintos mercados de forma conjunta y simultánea para toda la economía.

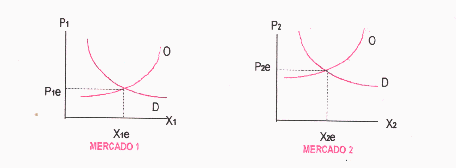
Una situación de equilibrio es aquella en la que la oferta y la demanda agregadas, coinciden en precio y cantidad. En un entorno competitivo, la situación de equilibrio se produce cuando no existen estímulos para que ninguno de los agentes económicos que operan en ese mercado este interesados en seguir operando.

Punto 1.- Comenzaremos estudiando un modelo sencillo de equilibrio general, en una economía de intercambio, en el que sólo existen dos consumidores (A,B) y dos bienes (X1,X2). Dada una asignación inicial de estos bienes, a través de un proceso de intercambio competitivo se agotarán las ganancias mutuamente beneficiosas que se derivan del comercio.

Una asignación es una distribución de estos bienes (X1 y X2), entre los dos consumidores (A y B).

Punto 2.- Después introduciremos la posibilidad de que haya producción, para lo que utilizaremos un modelo en el que sólo existen dos factores (K y L) y dos productores (E1 y E2) cuya oferta total es fija. Y veremos, que también en este caso, el intercambio competitivo explota todas las ganancias que se derivan del comercio.

Punto 3.- A continuación, veremos la tercera condición para lograr el equilibrio general competitivo, esto es, la consecución del equilibrio en el intercambio y en la producción de forma conjunta y simultáneamente.

Punto 4.- Por último, hablaremos de las externalidades y sus efectos sobre la eficacia en los mercados, así como sus diversas formas.

En una economía sencilla donde solo hay dos consumidores, el consumidor A, y el consumidor B y dos bienes, el bien X1, y el bien X2. Estos bienes no se producen en este ejemplo, sino que están dados, supongamos para nuestro análisis que existen en esta economía de intercambio 100 unidades del bien 1, y 50 unidades del bien 2.

Y supongamos una dotación inicial en la cual el consumidor A, tiene 70 unidades del bien 1, y 15 del bien 2. Y el consumidor B tiene 30 unidades del bien 1 y 35 del bien 2. Las opciones que tienen ambos agentes económicos son: bien consumir lo que tienen o bien realizar intercambios.

Estos intercambios sólo se producirán si mejora el bienestar de ambos. Un intercambio mejorará el bienestar del consumidor, si le permite a este situarse en una curva de indiferencia más alejada del origen, que la curva en que le sitúa la asignación inicial.

La caja de Edgeworth

Es una herramienta de análisis que consiste en analizar el intercambio de dos bienes entre dos consumidores, permite representar gráficamente las dotaciones y sus preferencias, permitiendo estudiar los diferentes resultados del proceso de intercambio. Partiremos del estudio de la estructura de dos familias de curvas independientes, girando una de ellas y formando una caja. El tamaño de la misma dependerá del consumo máximo que se puede realizar, es decir todo el bien existente. Los ejes de abscisas para el bien X1 y el de ordenadas para el bien X2.

A y B se reparten los bienes X1 y X2, atendiendo a su función de utilidad, y a las cantidades existentes en la economía:

UA = f (X1A , X2A)

UB = f (X1B , X2B)

X1 y X2 constantes.

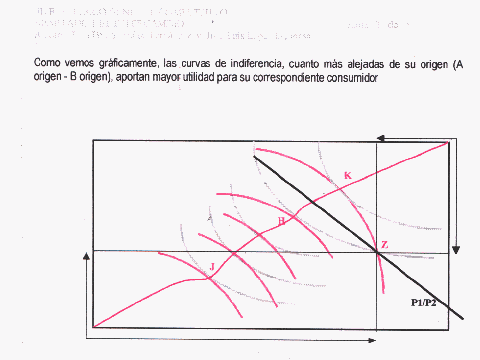
En la caja, vemos reflejada la denominada "curva de contrato", que es aquella que uno todos los puntos de tangencia entre las curvas de utilidad de los agentes (puntos de asignación eficientes) cuyo número es infinito. Dicho de otro modo, la curva de contrato identifica todas las maneras eficientes de asignar los dos bienes entre los dos consumidores. Por tanto, la característica principal de estos puntos es su igualdad en la Relación Marginal de Sustitución (RMS). Esto es:

RMSA = RMSB

Si "Z" -combinación inicial-, no fuese un punto de equilibrio, A y B harían intercambio, para lo que sería necesario encontrar una relación de intercambio, y esto es lo que el mercado hará de manera automática.

Los intercambios son puramente voluntarios, por lo que solo se realizaran si se mejora el bienestar de las dos partes. Un intercambio mejora el bienestar de una persona cuando la sitúa en una en una curva de indiferencia más alejada del origen.

Para A, es indiferente estar en el punto "Z" o en el punto "H", ya que ambos puntos están dentro de la misma curva de indiferencia, sin embargo al consumidor B le interesa pasar de "Z" a "H" ya que esto le sitúa en una curva de indiferencia superior.

Pero al mismo tiempo el consumidor A preferiría situarse en el punto "K" donde se colocaría en una curva de indiferencia superior que en el punto de dotación inicial "Z", y por el contrario, el consumidor B es indiferente entre estos dos puntos ya que ambos se encuentran dentro de la misma curva de indiferencia.

Por tanto, cualquier intercambio que se realice, quedará limitado entre los puntos "H" y "K", a esta área de nuestra caja de Edgeworth le denominaremos "límite del intercambio". Este límite vendrá determinado por los criterios de Pareto : preferido en sentido de Pareto y óptimo en el sentido de Pareto.

Como hemos visto los puntos "H" y "K" son preferidos en sentido de Pareto a la asignación inicial "Z", y también son óptimos en el sentido de Pareto (óptimo paretiano):

Decimos que una asignación es óptimo-paretiana ó eficiente en el sentido de Pareto a aquellas que cumplen:

1.- No es posible mejorar el bienestar de todos los individuos involucrados.

2.- No es posible mejorar el bienestar de una de ellas sin empeorar el de otra.

3.- Se han agotado todas las ganancias derivadas del comercio

4.- No es posible realizar ningún intercambio mutuamente ventajoso, etc...

Los criterios de Pareto son esencialmente relativos, cuando decimos que un punto como "J" -ver gráfico anterior- es un óptimo en el sentido de Pareto, no estamos diciendo que sea bueno en un sentido absoluto. Ya que para el consumidor A será difícil que sea satisfactorio, sus dotaciones son inferiores a las del consumidor B.

Por lo tanto los criterios de Pareto, sólo sirven en relación con las dotaciones iniciales. Estos en lugar de permanecer en la asignación inicial, deciden trasladarse a otra que se prefiera en el sentido de Pareto, y de hecho continúan trasladándose hasta alcanzar otra que sea óptima en el sentido de Pareto:

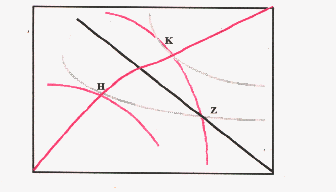
En la combinación inicial -punto "Z"- es un punto de desigualdad, en él, como hemos visto anteriormente no se produce las igualdades de las RMS, no es por tanto una asignación óptimo paretiana.

¿Cómo determinar sí la RMSA > ó < que RMSB ?

La idea nos la da la ecuación:

Partiendo de la asignación inicial : consumidor A, 70 unidades del bien 1 y 15 del bien 2.

En el punto "Z", el agente A esta dispuesto a entregar parte de bien 1 a cambio de conseguir más del bien 2, lo que indica que para A el bien 2 tiene una mayor utilidad que el bien 1. Para B, es justo lo contrario, faltará saber en que proporción.

Pasar de la combinación reflejada en el punto "Z" a "H" ó "K" dependerá de la relación de precios (P1/P2):

Punto "K"; P1/P21 = 1/10

Punto "H"; P1/P22 = 4/2

Pero entre estos puntos extremos, alguien al que llamaremos subastador, puede ofrecer una alternativa más aceptable. El subastador anuncia simplemente un nuevo cociente de precios, a esta nueva relación podría darse que:

Mientras la demanda del bien 1 fuese menor que su oferta, esto haría que su precio bajase, si sigue habiendo un exceso de oferta el subastador anuncia otro cociente de precios más alto, y así sucesivamente.

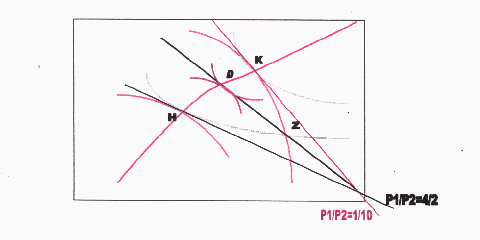
El punto "D" es un punto que sería un óptimo, porque es de equilibrio y además es un punto de la curva de contrato. Es un punto óptimo-paretiano hacia donde nos llevaría el mercado desde una asignación inicial "Z".

Veremos las condiciones necesarias para obtener el equilibrio a través de las variaciones de precio de los factores productivos. Y como con los consumidores, nuestra herramienta de análisis será la Caja de Edgeworth en los mercados de producción.

Seguiremos suponiendo que las cantidades totales de los dos factores son fijas e iguales a: K=50 ; L=100. Supongamos por último, que los procesos de producción utilizados por las dos empresas dan lugar a las isocuantas convencionales -de forma convexa-.

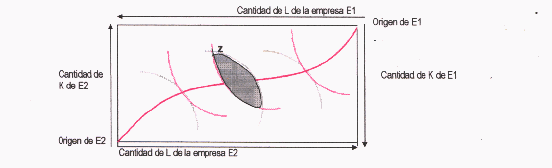
Partiendo de una asignación inicial "Z", podemos hacernos dos preguntas:

¿es esta una situación de equilibrio?

¿es esta una situación óptimo-paretiana?

Sabemos que esta asignación no puede ser eficiente, porque podemos desplazarnos a cualquier punto del área sombreada -límites de intercambio a la producción- y conseguir más unidades de los dos bienes.

La curva de contrato de la producción es el conjunto de puntos técnicamente eficientes en la producción, dicho de otro modo, es el conjunto de puntos de tangencia de las isocuantas. Como sabemos, la pendiente de una isocuanta en cualquier punto se denomina "relación marginal de sustitución técnica (RMST)" en ese punto.

La RMST es la relación a la que puede intercambiarse trabajo (L) por capital (K) sin alterar la cantidad total de producción. Debemos observar que la RMST entre K y L debe ser la misma para las dos empresas en todos los puntos de la curva de contrato de la producción.:

La relación de precios determinará la cantidad de trabajo y capital que las empresas estén dispuestas a intercambiar, hasta encontrar un punto como "P" donde se equilibre el mercado. Este punto será el denominado punto de equilibrio, donde encontraremos que:

Ya hemos vistos dos de las condiciones necesarias para el equilibrio general competitivo:

En este apartado veremos la tercera condición, que es la más importante a la vez que la más difícil de demostrar. Y es el hecho de que las dos condiciones anteriores se den de forma conjunta y simultánea

Una economía podría ser eficiente en la producción y en el consumo y, sin embargo, satisfacer inadecuadamente las necesidades de sus agentes. Eso podría ocurrir, por ejemplo, en el caso de que se dedicará por alguna razón todos los recursos a la producción de uno de los bienes, y nada a la del otro. Los factores podrían estar asignados eficientemente en la producción de esta desequilibrada combinación de bienes. Pero todos los agentes de esta economía, desearían que hubiese una distribución diferente en la combinación de bienes. Por lo tanto, existe otro criterio que tiene interés para conocer el grado de eficiencia de una economía, esto es, si es eficiente la combinación de bienes que en ella se produce.

Para definir la combinación de bienes eficiente, resulta útil traducir la curva de contrato en la caja de Edgeworth en la producción, en una frontera de posibilidades de producción -FPP-; que es el conjunto de todas las combinaciones posibles de producción que pueden obtenerse con unas cantidades dadas de los factores (K, L). Todos los puntos de la curva de contrato dan lugar a cantidades específicas del bien 1 y el bien 2.

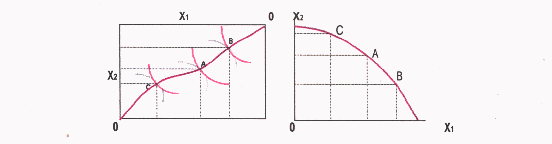
La forma cóncava de la frontera de posibilidades de producción viene explicada por la "ley de productividades marginales decrecientes". A medida que reducimos unidades de capital de un proceso productivo donde se emplea mucho capital, y se emplea en otro proceso donde había poco, este capital pasará de ser poco productivo en el primer proceso a ser más productivo en el segundo. En la medida en que las dos funciones de producción tenga rendimientos decrecientes o constantes a escala, la frontera de posibilidades de producción no puede ser convexa desde el origen.

Para que una economía sea eficiente en lo referido a su combinación de productos es necesario que la relación marginal de sustitución de uno de los consumidores sea igual a la relación marginal de transformación (RMS = RMT).

Por lo tanto la combinación inicial de productos no podía ser eficiente, recordemos que eficiente significa óptimo en el sentido de Pareto.

Ahora lo que se plantea es cuánto se produce de cada uno de los productos, ya que quien decide lo que se produce son los consumidores a través del vector de precios.

La curva de posibilidades de producción representa lo mismo que la curva de contrato en la caja de Edgeworth, es decir, todas las combinaciones eficientes. Cualquier combinación sobre la FPP, implica que no se puede ampliar la producción de la Empresa 1 sin reducir la producción de la Empresa 2. La cantidad global de factores productivos (K,L), determinan el tamaño de la curva de posibilidades de producción.

El mecanismo que permite que los productores maximicen sus beneficios, atendiendo a las necesidades de los consumidores son los precios. La señal de los precios indica que los consumidores están dispuestos a pagar más por aquello que maximiza su utilidad.

Las condiciones para esto son que deba darse en primer lugar que la RMT en este punto de la frontera de posibilidades de producción -FPP- sea igual al cociente entre costes marginales de los productos:

También sabemos que la condición de equilibrio de los productores competitivos de X1 y X2, es que los precios de los productos sean iguales a los costes marginales:

P1 / P2 = CmgX1 / CmgX2

Lo que quiere decir que el cociente entre los precios de equilibrio de los productos es, de hecho, igual a su relación marginal de transformación.

En concreto, hemos demostrado que una economía que se encuentre en equilibrio general competitivo, será en determinadas condiciones, eficiente -en el sentido de Pareto- en el consumo, en la producción y en la elección de la combinación de productos. Como ya hemos visto, una sociedad cuya asignación de recursos sea óptima en el sentido de Pareto, no tiene porque ser necesariamente una buena sociedad. El equilibrio último del mercado depende en buena medida de la distribución de las dotaciones iniciales, y si esta distribución no es justa, no hay razón alguna para esperar que lo sea el equilibrio competitivo.

4 LA EXTERNALIDADES

Llegado a este punto de nuestro estudio, hemos de hacer una serie de apreciaciones, por lo visto hasta ahora, mediante la eficiencia en la economía se produce lo necesario asignándolo al consumidor según su utilidad. Pero esta eficiencia se mide a través de los precios, lo que deja al margen conceptos a tener en cuenta como el de equidad en la distribución:

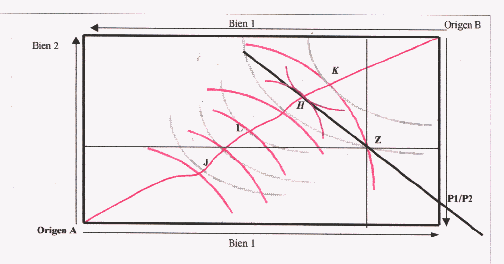
Como podemos observar en el gráfico anterior, el punto L, será probablemente más equitativo para los agentes de la economía, pero el sistema de precios nunca nos llevaría a este punto , sino al de equilibrio general -punto H-.

Esta es una buena razón para la intervención en el mercado, aunque no la única. En este capítulo veremos algunas de las razones de intervención, como pueden ser:

Esto nos lleva a observar diferentes mecanismos de esta intervención, como pueden ser: el establecimiento de normas y leyes que rijan la economía y garanticen una distribución más equitativa, el presupuesto como herramienta de redistribución, la prestación directa de bienes públicos -exeternalidad positiva- ...

• Los impuestos

Como vimos en el apartado anterior, la economía se halla en condiciones de equilibrio general competitivo en un punto como B. En el cual la relación marginal de transformación es igual al cociente entre los precios de los productos correspondientes al equilibrio competitivo, P1/P2.

Supongamos ahora que introducimos un impuesto gravando el bien X2, a un tipo impositivo (t) por unidad monetaria. Cada vez que un productor vende una unidad de X2 al precio P2, sólo se quedará con (1-t)*P2. La consecuencia inmediata del impuesto es un aumento del cociente entre los precios relativos, pasando de:

Los productores, que antes producían en el punto B de la -FPP-, ahora observan que pueden obtener un mayor beneficio o reducir sus pérdidas produciendo en otro punto de la -FPP- donde se produce una mayor cantidad de X1 y una menor cantidad de X2. Y por tanto en este nuevo punto la RMT > RMS, lo que significa que la economía ya no tendrá una combinación de productos eficiente. La asignación inicial situada en B era óptima en el sentido de Pareto, la nueva asignación tiene una cantidad demasiado elevada de X1 y pequeña de X2.

Las subvenciones al igual que los impuestos, alteran las condiciones necesarias para que exista eficiencia. Esto no quiere decir que el mundo disfrutaría de un mayor bienestar si se abolieran todos los impuestos, ya que difícilmente en un mundo de ese tipo el Estado podría suministrar ningún tipo de bienes y servicios. Y sin embargo, hay muchos bienes y servicios valiosos que sería improbable que se suministrasen de ninguna otra forma.

La conclusión del análisis del equilibrio general es que hemos de procurar que los impuestos que se diseñen creen las menores distorsiones posibles.

• El monopolio

Los impuestos no son sino uno de los numerosos factores que impiden lograr una asignación óptima de los recursos en el sentido de Pareto. Otra fuente de ineficiencia es el monopolio, cuyas consecuencias para el equilibrio general son muy parecidas a las de un impuesto sobre las mercancías/productos.

El productor competitivo selecciona un nivel de producción en el que el coste marginal es igual al precio; el monopolista selecciona uno en el que el coste marginal es igual al ingreso marginal. Dado que el precio siempre es superior al ingreso marginal en una curva de demanda de pendiente negativa, significa que el precio será superior al coste marginal en el caso del monopolista.

• Externalidades

Existe otra fuente de ineficiencia, cuando la producción o el consumo implican beneficios o costes que recaen en personas que no intervienen directamente en estas actividades. Estos beneficios y costes suelen denominarse externalidades.

Un ejemplo habitual de externalidad negativa, es el caso de la contaminación, en el cual una actividad productiva provoca emisiones contaminantes que afectan negativamente a personas que no son las que consumen el producto.

En el caso de externalidad negativa de la producción, las consecuencias para la eficiencia son parecidas a las de una subvención. El productor cuando se pregunta que cantidad debe producir, iguala el precio a su propio coste marginal privado. El problema se halla, en que las externalidades negativas imponen costes adicionales a otros, que no son tenidos en cuenta por el productor.

• Bienes públicos

Otro factor que impide lograr asignaciones eficientes a través de los mercados privados, es la existencia de bienes públicos. Un bien público puro es aquel que tiene dos propiedades específicas:

• no puede disminuir, lo que significa que su utilización por parte de una persona no reduce la cantidad de que disponen los demás.
• no es excluíble, lo que significa que es imposible incluir que lo utilicen las personas que no lo pagan. Por ejemplo, antes que se inventarán los codificadores de canales televisivos, las emisiones de televisión eran un ejemplo de bien público.